

Picture by Writer
Outliers are irregular observations that differ considerably from the remainder of your information. They might happen resulting from experimentation error, measurement error, or just that variability is current throughout the information itself. These outliers can severely influence your mannequin’s efficiency, resulting in biased outcomes – very similar to how a prime performer in relative grading at universities can elevate the common and have an effect on the grading standards. Dealing with outliers is an important a part of the info cleansing process.
On this article, I will share how one can spot outliers and other ways to cope with them in your dataset.
Detecting Outliers
There are a number of strategies used to detect outliers. If I had been to categorise them, right here is the way it appears to be like:
- Visualization-Primarily based Strategies: Plotting scatter plots or field plots to see information distribution and examine it for irregular information factors.
- Statistics-Primarily based Strategies: These approaches contain z scores and IQR (Interquartile Vary) which supply reliability however could also be much less intuitive.
I will not cowl these strategies extensively to remain targeted, on the subject. Nonetheless, I will embrace some references on the finish, for exploration. We’ll use the IQR technique in our instance. Right here is how this technique works:
IQR (Interquartile Vary) = Q3 (seventy fifth percentile) – Q1 (twenty fifth percentile)
The IQR technique states that any information factors beneath Q1 – 1.5 * IQR or above Q3 + 1.5 * IQR are marked as outliers. Let’s generate some random information factors and detect the outliers utilizing this technique.
Make the required imports and generate the random information utilizing np.random:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Generate random information
np.random.seed(42)
information = pd.DataFrame({
'worth': np.random.regular(0, 1, 1000)
})
Detect the outliers from the dataset utilizing the IQR Technique:
# Operate to detect outliers utilizing IQR
def detect_outliers_iqr(information):
Q1 = information.quantile(0.25)
Q3 = information.quantile(0.75)
IQR = Q3 - Q1
lower_bound = Q1 - 1.5 * IQR
upper_bound = Q3 + 1.5 * IQR
return (information < lower_bound) | (information > upper_bound)
# Detect outliers
outliers = detect_outliers_iqr(information['value'])
print(f"Variety of outliers detected: {sum(outliers)}")
Output ⇒ Variety of outliers detected: 8
Visualize the dataset utilizing scatter and field plots to see the way it appears to be like
# Visualize the info with outliers utilizing scatter plot and field plot
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(information)), information['value'], c=['blue' if not x else 'red' for x in outliers])
ax1.set_title('Dataset with Outliers Highlighted (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=information['value'], ax=ax2)
ax2.set_title('Dataset with Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()
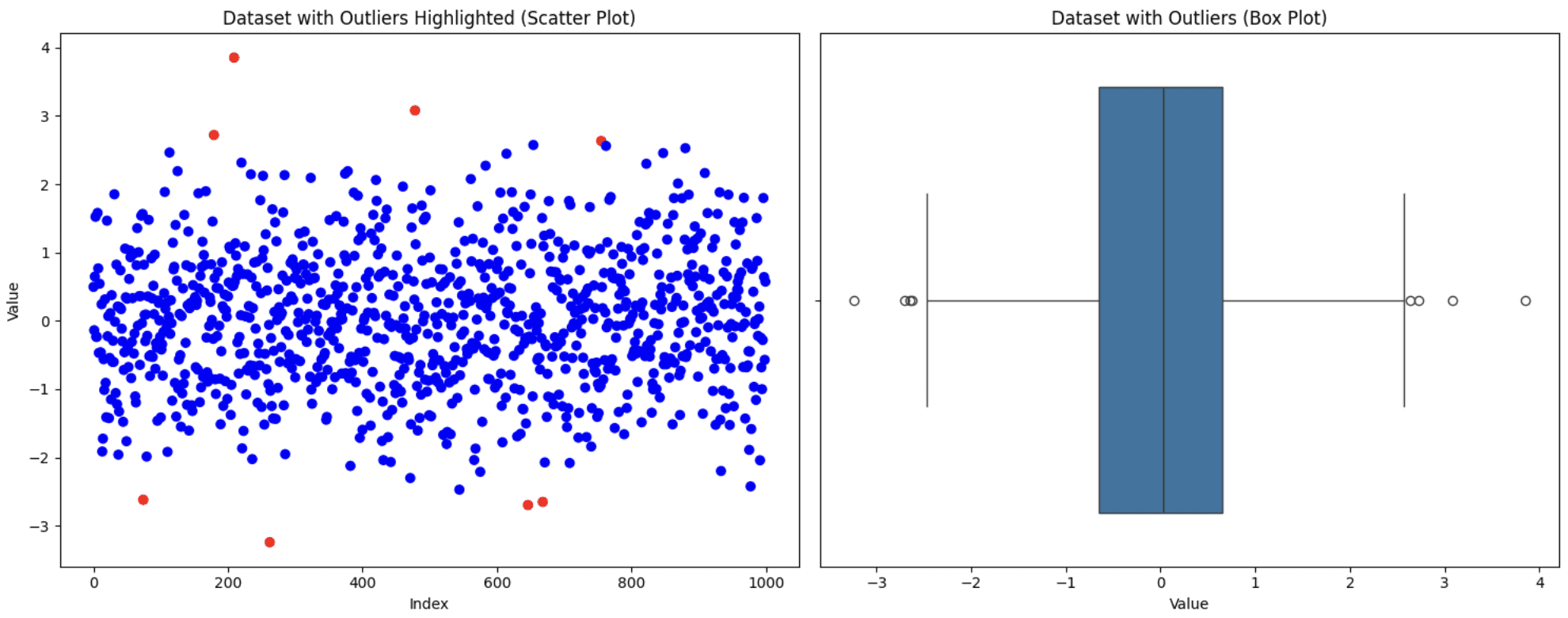

Unique Dataset
Now that we’ve got detected the outliers, let’s talk about among the other ways to deal with the outliers.
Dealing with Outliers
1. Eradicating Outliers
This is without doubt one of the easiest approaches however not at all times the best one. It is advisable to take into account sure elements. If eradicating these outliers considerably reduces your dataset measurement or in the event that they maintain worthwhile insights, then excluding them out of your evaluation not be essentially the most favorable resolution. Nonetheless, in the event that they’re resulting from measurement errors and few in quantity, then this strategy is appropriate. Let’s apply this system to the dataset generated above:
# Take away outliers
data_cleaned = information[~outliers]
print(f"Unique dataset measurement: {len(information)}")
print(f"Cleaned dataset measurement: {len(data_cleaned)}")
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(data_cleaned)), data_cleaned['value'])
ax1.set_title('Dataset After Eradicating Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=data_cleaned['value'], ax=ax2)
ax2.set_title('Dataset After Eradicating Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()
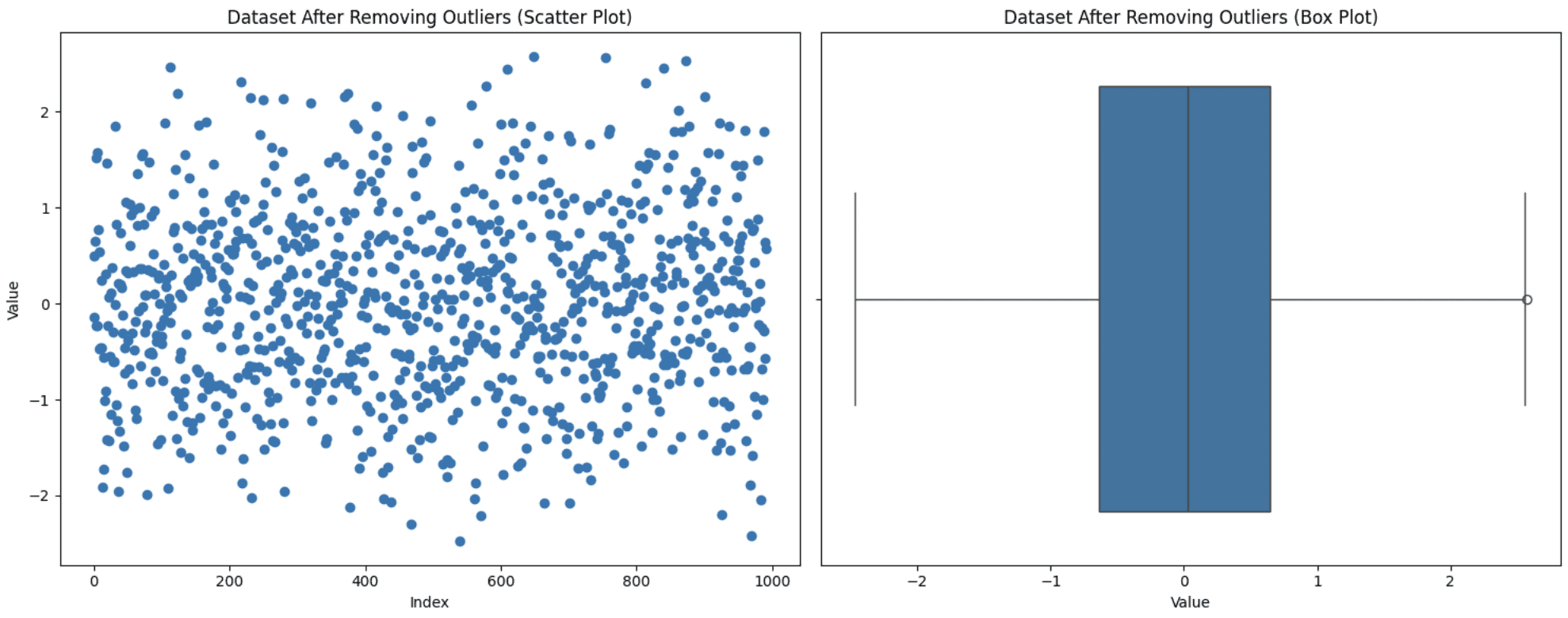

Eradicating Outliers
Discover that the distribution of the info can really be modified by eradicating outliers. For those who take away some preliminary outliers, the definition of what’s an outlier could very nicely change. Due to this fact, information that might have been within the regular vary earlier than, could also be thought of outliers beneath a brand new distribution. You’ll be able to see a brand new outlier with the brand new field plot.
2. Capping Outliers
This method is used when you don’t want to discard your information factors however protecting these excessive values can even influence your evaluation. So, you set a threshold for the utmost and the minimal values after which deliver the outliers inside this vary. You’ll be able to apply this capping to outliers or to your dataset as an entire too. Let’s apply the capping technique to our full dataset to deliver it throughout the vary of the Fifth-Ninety fifth percentile. Right here is how one can execute this:
def cap_outliers(information, lower_percentile=5, upper_percentile=95):
lower_limit = np.percentile(information, lower_percentile)
upper_limit = np.percentile(information, upper_percentile)
return np.clip(information, lower_limit, upper_limit)
information['value_capped'] = cap_outliers(information['value'])
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(information)), information['value_capped'])
ax1.set_title('Dataset After Capping Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=information['value_capped'], ax=ax2)
ax2.set_title('Dataset After Capping Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()
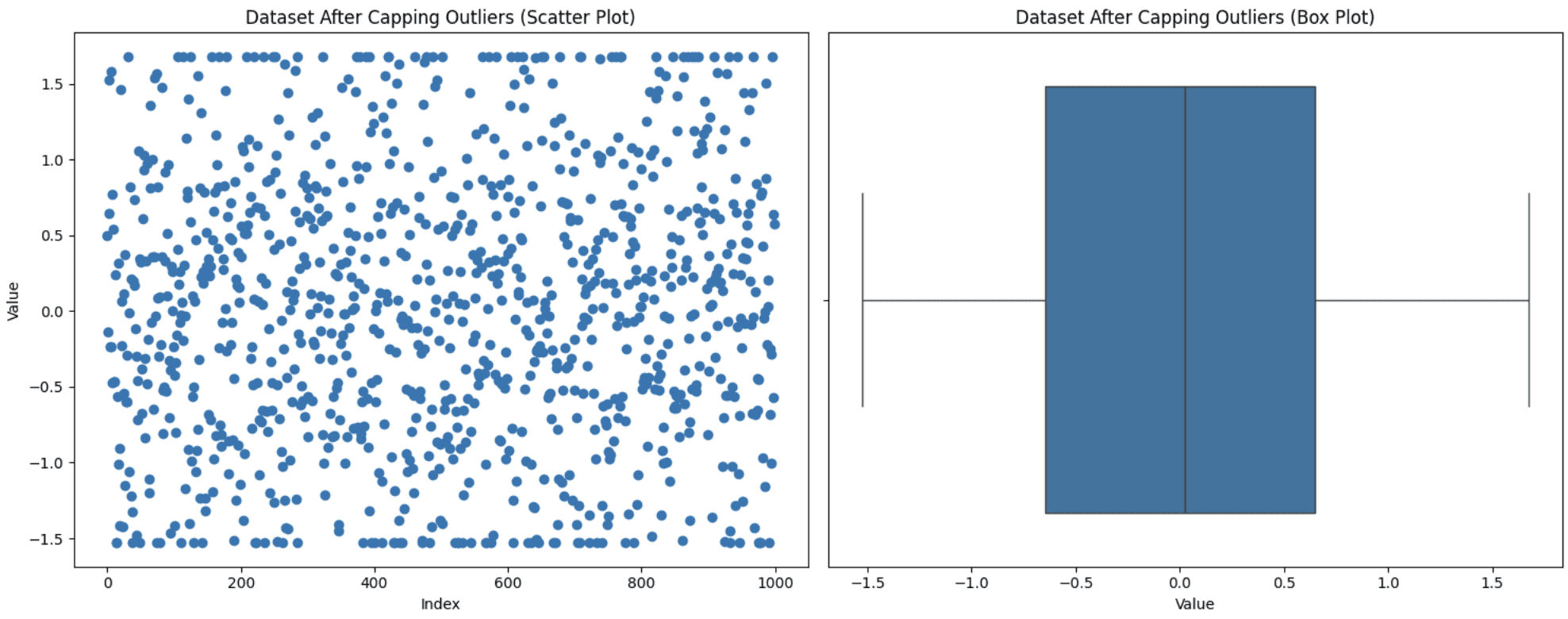

Capping Outliers
You’ll be able to see from the graph that the higher and decrease factors within the scatter plot seem like in a line resulting from capping.
3. Imputing Outliers
Generally eradicating values from the evaluation is not an choice as it might result in data loss, and also you additionally don’t desire these values to be set to max or min like in capping. On this scenario, one other strategy is to substitute these values with extra significant choices like imply, median, or mode. The selection varies relying on the area of knowledge beneath statement, however be aware of not introducing biases whereas utilizing this system. Let’s change our outliers with the mode (essentially the most steadily occurring worth) worth and see how the graph seems:
information['value_imputed'] = information['value'].copy()
median_value = information['value'].median()
information.loc[outliers, 'value_imputed'] = median_value
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(15, 6))
# Scatter plot
ax1.scatter(vary(len(information)), information['value_imputed'])
ax1.set_title('Dataset After Imputing Outliers (Scatter Plot)')
ax1.set_xlabel('Index')
ax1.set_ylabel('Worth')
# Field plot
sns.boxplot(x=information['value_imputed'], ax=ax2)
ax2.set_title('Dataset After Imputing Outliers (Field Plot)')
ax2.set_xlabel('Worth')
plt.tight_layout()
plt.present()
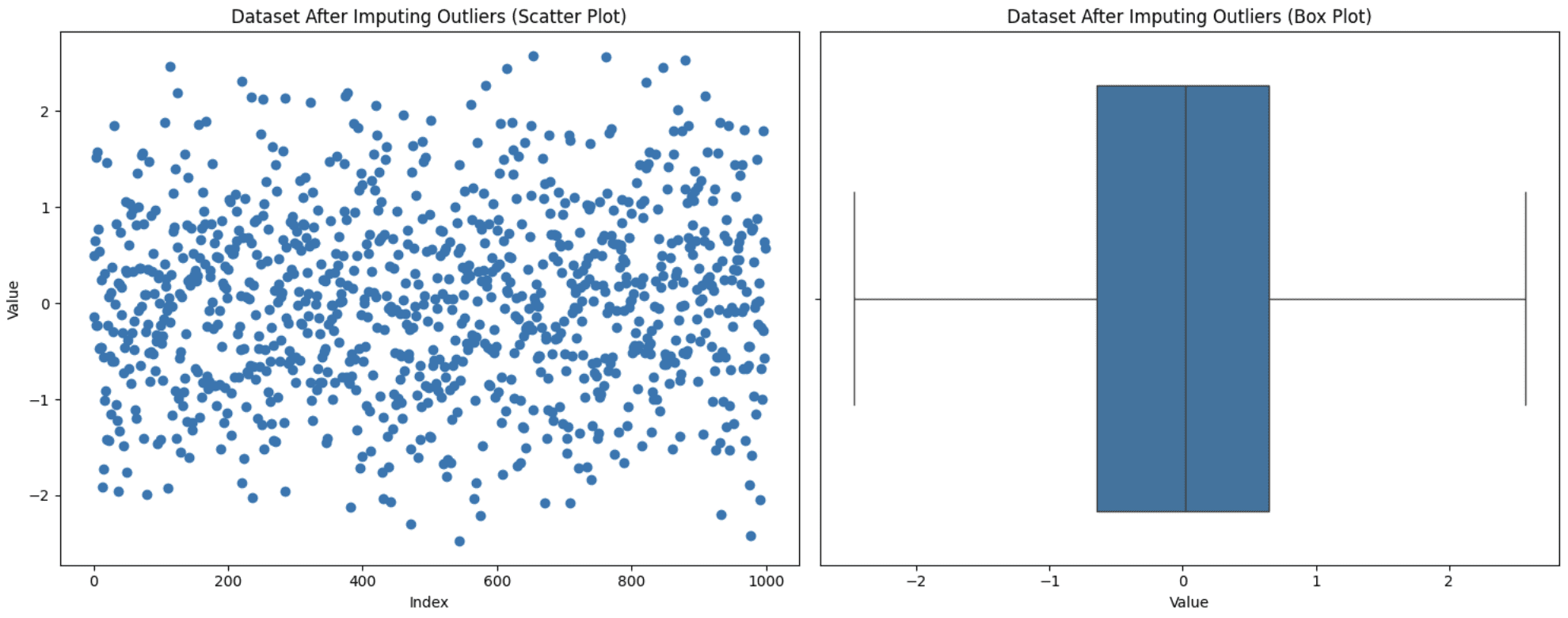

Imputing Outliers
Discover that now we haven’t any outliers, however this does not assure that outliers can be eliminated since after the imputation, the IQR additionally adjustments. It is advisable to experiment to see what matches finest on your case.
4. Making use of a Transformation
Transformation is utilized to your full dataset as a substitute of particular outliers. You principally change the way in which your information is represented to scale back the influence of the outliers. There are a number of transformation strategies like log transformation, sq. root transformation, box-cox transformation, Z-scaling, Yeo-Johnson transformation, min-max scaling, and many others. Selecting the best transformation on your case will depend on the character of the info and your finish objective of the evaluation. Listed below are just a few suggestions that will help you choose the best transformation approach:
- For right-skewed information: Use log, sq. root, or Field-Cox transformation. Log is even higher while you need to compress small quantity values which might be unfold over a big scale. Sq. root is healthier when, other than proper skew, you need a much less excessive transformation and in addition need to deal with zero values, whereas Field-Cox additionally normalizes your information, which the opposite two do not.
- For left-skewed information: Replicate the info first after which apply the strategies talked about for right-skewed information.
- To stabilize variance: Use Field-Cox or Yeo-Johnson (just like Field-Cox however handles zero and adverse values as nicely).
- For mean-centering and scaling: Use z-score standardization (normal deviation = 1).
- For range-bound scaling (mounted vary i.e., [2,5]): Use min-max scaling.
Let’s generate a right-skewed dataset and apply the log transformation to the whole information to see how this works:
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
# Generate right-skewed information
np.random.seed(42)
information = np.random.exponential(scale=2, measurement=1000)
df = pd.DataFrame(information, columns=['value'])
# Apply Log Transformation (shifted to keep away from log(0))
df['log_value'] = np.log1p(df['value'])
fig, axes = plt.subplots(2, 2, figsize=(15, 10))
# Unique Information - Scatter Plot
axes[0, 0].scatter(vary(len(df)), df['value'], alpha=0.5)
axes[0, 0].set_title('Unique Information (Scatter Plot)')
axes[0, 0].set_xlabel('Index')
axes[0, 0].set_ylabel('Worth')
# Unique Information - Field Plot
sns.boxplot(x=df['value'], ax=axes[0, 1])
axes[0, 1].set_title('Unique Information (Field Plot)')
axes[0, 1].set_xlabel('Worth')
# Log Remodeled Information - Scatter Plot
axes[1, 0].scatter(vary(len(df)), df['log_value'], alpha=0.5)
axes[1, 0].set_title('Log Remodeled Information (Scatter Plot)')
axes[1, 0].set_xlabel('Index')
axes[1, 0].set_ylabel('Log(Worth)')
# Log Remodeled Information - Field Plot
sns.boxplot(x=df['log_value'], ax=axes[1, 1])
axes[1, 1].set_title('Log Remodeled Information (Field Plot)')
axes[1, 1].set_xlabel('Log(Worth)')
plt.tight_layout()
plt.present()


Making use of Log Transformation
You’ll be able to see {that a} easy transformation has dealt with a lot of the outliers itself and lowered them to only one. This exhibits the ability of transformation in dealing with outliers. On this case, it’s essential to be cautious and know your information nicely sufficient to decide on applicable transformation as a result of failing to take action could trigger issues for you.
Wrapping Up
This brings us to the top of our dialogue about outliers, other ways to detect them, and the best way to deal with them. This text is a part of the pandas collection, and you’ll verify different articles on my creator web page. As talked about above, listed below are some further sources so that you can research extra about outliers:
- Outlier detection strategies in Machine Studying
- Totally different transformations in Machine Studying
- Varieties Of Transformations For Higher Regular Distribution
Kanwal Mehreen Kanwal is a machine studying engineer and a technical author with a profound ardour for information science and the intersection of AI with drugs. She co-authored the e-book «Maximizing Productiveness with ChatGPT». As a Google Era Scholar 2022 for APAC, she champions range and tutorial excellence. She’s additionally acknowledged as a Teradata Range in Tech Scholar, Mitacs Globalink Analysis Scholar, and Harvard WeCode Scholar. Kanwal is an ardent advocate for change, having based FEMCodes to empower girls in STEM fields.
