Los modelos de educación profundo se basan en funciones de activación que proporcionan no linealidad y permiten a las redes asimilar patrones complicados. Este artículo analizará la función de activación de Softplus, qué es y cómo se puede usar en PyTorch. Se puede aseverar que Softplus es una forma fluida de la popular activación de ReLU, que mitiga los inconvenientes de ReLU pero introduce sus propios inconvenientes. Discutiremos qué es Softplus, su fórmula matemática, su comparación con ReLU, cuáles son sus ventajas y limitaciones y daremos un paseo por poco de código PyTorch usándolo.
¿Qué es la Función de Activación de Softplus?
La función de activación Softplus es una función no directo de redes neuronales y se caracteriza por una acercamiento suave de la función ReLU. En palabras más sencillas, Softplus actúa como ReLU en los casos en que la entrada positiva o negativa es muy extenso, pero no hay una arista afilada en el punto cero. En su ocasión, aumenta suavemente y produce una producción insignificante positiva frente a insumos negativos en ocasión de un cero firme. Este comportamiento continuo y diferenciable implica que Softplus es continuo y diferenciable en todas partes en contraste con ReLU que es discontinuo (con un cambio imprevisto de irresoluto) en x = 0.
¿Por qué se utiliza Softplus?
Softplus es seleccionado por desarrolladores que prefieren la activación más conveniente que ofrece. gradientes distintos de cero incluso donde ReLU estaría inactivo. La optimización basada en gradientes puede evitar interrupciones importantes causadas por la suavidad de Softplus (el gradiente cambia suavemente en ocasión de escalonar). Todavía recorta inherentemente las panorama (como lo hace ReLU), pero el recortadura no es cero. En prontuario, Softplus es la lectura más suave de ReLU: es similar a ReLU cuando el valía es extenso pero es mejor rodeando de cero y es agradable y fluido.
Fórmula Matemática Softplus
El Softplus se define matemáticamente como:
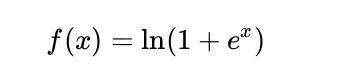
Cuando nudo es extenso, minudo es muy extenso y por lo tanto, ln(1 + minudo) es muy similar a en(e)nudo)igual a nudo. Implica que Softplus es casi directo en entradas grandes, como ReLU.
Cuando nudo es extenso y imagen, minudo es muy pequeño, por lo tanto ln(1 + minudo) es casi en(1)y esto es 0. Los títulos producidos por Softplus son cercanos a cero pero nunca cero. Para tomar un valía que sea cero, x debe tender a infinito imagen.
Otra cosa útil es que la derivada de Softplus es el sigmoide. La derivada de ln(1 + minudo) es:
minudo / (1 + minudo)
Este es el mismo sigmoideo de nudo. Implica que en cualquier momento la irresoluto de Softplus es sigmoideo(x)es aseverar, tiene un gradiente diferente de cero en todas partes y es suave. Esto hace que Softplus sea útil en el educación basado en gradientes, ya que no tiene áreas planas donde los gradientes desaparecen.
Usando Softplus en PyTorch
PyTorch proporciona la activación Softplus como activación nativa y, por lo tanto, puede estilarse fácilmente como ReLU o cualquier otra activación. A continuación se ofrece un ejemplo de dos simples. El primero utiliza Softplus en una pequeña cantidad de títulos de prueba, y el segundo demuestra cómo insertar Softplus en un pequeño red neuronal.
Softplus en entradas de muestra
El posterior fragmento se aplica nn.Softplus a un tensor pequeño para que puedas ver cómo se comporta con entradas negativas, cero y positivas.
import torch
import torch.nn as nn
# Create the Softplus activation
softplus = nn.Softplus() # default beta=1, threshold=20
# Sample inputs
x = torch.tensor((-2.0, -1.0, 0.0, 1.0, 2.0))
y = softplus(x)
print("Input:", x.tolist())
print("Softplus output:", y.tolist())
Lo que esto muestra:
- En x = -2 y x = -1, el valía de Softplus son títulos positivos pequeños en ocasión de 0.
- La salida es aproximadamente 0,6931 en x =0, es aseverar en(2)
- En caso de entradas positivas como 1 o 2, los resultados son un poco mayores que las entradas ya que Softplus suaviza la curva. Softplus se acerca a x a medida que aumenta.
El Softplus de PyTorch está representado por la fórmula ln(1 + exp(betax)). Su valía puertas interno de 20 es para evitar un desbordamiento aritmético. Softplus es directo en betax extenso, lo que significa que en ese caso PyTorch simplemente devuelve nudo.
Usando Softplus en una red neuronal
Aquí hay una red PyTorch simple que utiliza Softplus como activación para su capa oculta.
import torch
import torch.nn as nn
class SimpleNet(nn.Module):
def __init__(self, input_size, hidden_size, output_size):
super(SimpleNet, self).__init__()
self.fc1 = nn.Linear(input_size, hidden_size)
self.activation = nn.Softplus()
self.fc2 = nn.Linear(hidden_size, output_size)
def forward(self, x):
x = self.fc1(x)
x = self.activation(x) # apply Softplus
x = self.fc2(x)
return x
# Create the model
model = SimpleNet(input_size=4, hidden_size=3, output_size=1)
print(model)
Suceder una entrada a través del maniquí funciona como de costumbre:
x_input = torch.randn(2, 4) # batch of 2 samples
y_output = model(x_input)
print("Input:n", x_input)
print("Output:n", y_output)
En esta disposición, se utiliza la activación Softplus para que los títulos que salen de la primera capa a la segunda capa no sean negativos. La sustitución de Softplus por un maniquí existente no podrá faltar ninguna otra variación estructural. Sólo es importante recapacitar que Softplus puede ser un poco más moroso en el entrenamiento y requerir más cálculo que ReLU.
La capa final incluso se puede implementar con Softplus cuando hay títulos positivos que un maniquí debería gestar como panorama, por ejemplo, parámetros de escalera u objetivos de regresión positivos.
Softplus vs ReLU: tabla comparativa
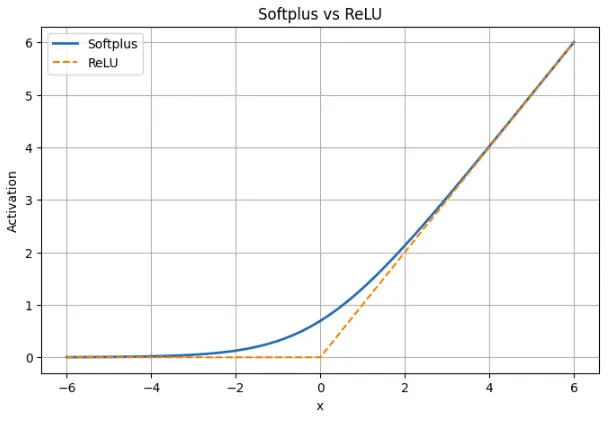
| Aspecto | Softplus | ReLU |
|---|---|---|
| Definición | f(x) = ln(1 + minudo) | f(x) = máx(0, x) |
| Forma | Transición suave en todos los x | Torcedura aguda en x = 0 |
| Comportamiento para x < 0 | Pequeño resultado positivo; nunca llega a cero | La salida es exactamente cero. |
| Ejemplo en x = -2 | Softplus ≈ 0,13 | ReLU = 0 |
| Cerca de x = 0 | Suave y diferenciable; valía ≈ 0,693 | No diferenciable en 0 |
| Comportamiento para x > 0 | Casi directo, se acerca mucho a ReLU | Recto con irresoluto 1 |
| Ejemplo en x = 5 | Softplus ≈ 5.0067 | ReLU = 5 |
| Gradiente | Siempre diferente de cero; derivada es sigmoide (x) | Cero para x < 0, indefinido en 0 |
| Peligro de neuronas muertas | Nadie | Posible para entradas negativas |
| Escasez | No produce ceros exactos | Produce ceros verdaderos |
| Sorpresa de entrenamiento | Flujo de gradiente estable, actualizaciones más fluidas | Simple pero puede dejar de asimilar para algunas neuronas. |
Un análogo de ReLU es softplus. Es ReLU con entradas positivas o negativas muy grandes pero con la arista en cero eliminada. Esto evita que las neuronas mueran ya que el gradiente no llega a cero. Esto tiene el precio de que Softplus no genera ceros verdaderos, lo que significa que no es tan escaso como ReLU. Softplus proporciona dinámicas de entrenamiento más cómodas en la destreza, pero ReLU se sigue utilizando porque es más rápido y sencillo.
Beneficios de usar Softplus
Softplus tiene algunos beneficios prácticos que lo hacen útil en algunos modelos.
- En todas partes suave y diferenciable.
No hay esquinas afiladas en Softplus. Es completamente diferenciable para cada entrada. Esto ayuda a apoyar gradientes que pueden terminar facilitando un poco la optimización, ya que la pérdida varía más lentamente.
- Evita las neuronas muertas
ReLU puede evitar la puesta al día cuando una neurona recibe continuamente entradas negativas, ya que el gradiente será cero. Softplus no da el valía cero exacto en números negativos y por lo tanto todas las neuronas permanecen parcialmente activas y se actualizan en el gradiente.
- Reacciona más favorablemente a entradas negativas.
Softplus no descarta las entradas negativas generando un valía cero como lo hace ReLU, sino que genera un pequeño valía positivo. Esto permite que el maniquí retenga una parte de la información de las señales negativas en ocasión de perderla toda.
En prontuario, Softplus mantiene el flujo de gradientes, previene la asesinato de neuronas y ofrece un comportamiento fluido para ser utilizado en algunas arquitecturas o tareas donde la continuidad es importante.
Limitaciones y compensaciones de Softplus
Todavía existen desventajas de Softplus que restringen la frecuencia de su uso.
- Más caro de calcular
Softplus utiliza operaciones exponenciales y logarítmicas que son más lentas que las simples max(0, x) de ReLU. Esta sobrecarga adicional se puede percibir visiblemente en modelos grandes porque ReLU está extremadamente optimizado en la mayoría del hardware.
- No hay verdadera escasez
ReLU genera ceros perfectos en ejemplos negativos, lo que puede economizar tiempo de cálculo y, en ocasiones, ayudar en la regularización. Softplus no da un cero existente y por lo tanto todas las neuronas no siempre están inactivas. Esto elimina el peligro de neuronas muertas, así como las ventajas de eficiencia de las activaciones escasas.
- Parar gradualmente la convergencia de redes profundas.
ReLU se usa comúnmente para entrenar modelos profundos. Tiene un contorno pronunciado y una región positiva directo que puede forzar el educación. Softplus es más fluido y puede tener actualizaciones lentas, especialmente en redes muy profundas donde la diferencia entre capas es pequeña.
En prontuario, Softplus tiene buenas propiedades matemáticas y evita problemas como neuronas muertas, pero estos beneficios no siempre se traducen en mejores resultados en redes profundas. Se utiliza mejor en casos donde la suavidad o los resultados positivos son importantes, en ocasión de como un reemplazo universal para ReLU.
Conclusión
Softplus proporciona alternativas suaves y fluidas de ReLU a las redes neuronales. Aprende gradientes, no mata neuronas y es completamente diferenciable en todas las entradas. Es como ReLU en títulos grandes, pero en cero, se comporta más como una constante que ReLU porque produce una salida y una irresoluto distintas de cero. Mientras tanto, está asociado con compensaciones. Todavía es más moroso de calcular; Siquiera genera ceros reales y es posible que no acelere el educación en redes profundas tan rápido como ReLU. Softplus es más efectivo en modelos donde los gradientes son suaves o donde las panorama positivas son obligatorias. En la mayoría de los demás escenarios, es una alternativa útil al reemplazo predeterminado de ReLU.
Preguntas frecuentes
R. Softplus previene las neuronas muertas al apoyar gradientes distintos de cero para todas las entradas, lo que ofrece una alternativa fluida a ReLU y al mismo tiempo se comporta de forma similar para títulos positivos grandes.
R. Es una buena opción cuando su maniquí se beneficia de gradientes suaves o debe gestar títulos estrictamente positivos, como parámetros de escalera o ciertos objetivos de regresión.
R. Es más moroso de calcular que ReLU, no crea activaciones escasas y puede provocar una convergencia tenuemente más lenta en redes profundas.
Inicie sesión para continuar leyendo y disfrutar de contenido seleccionado por expertos.
